Grünova, Lehrmittel für die Schule

"Ebene Geometrie"

...eines von vielen Beispielen...

Demonstrationsbeispiel:

Formelerarbeitung
durch Umlegen.

Animation durch Anklicken
des Drachen starten!

"Drachenviereck"

e x f
2

Bei diesem Satz legen wir vor allem Wert auf allgemein verständliche Herleitungen. Experimentell induktiv soll der Geometrieunterricht praktiziert werden. Die Ausstattung ist deshalb so zusammengesetzt, dass man alle zu behandelnden Figuren aus bereits bekannten Flächen durch "Umformen, Umgruppieren, Umlegen" aufbaut. Auf diese Weise gelangt man über das Experiment zur Formelfindung. Mühelos kann man aus einem Rechteck zu einem Dreieck, Parallelogramm, Trapez, Drachenviereck oder allgemeinen Viereck übergehen.

Dieses Spitzenprodukt aus dem Hause GRÜNOVA beinhaltet die komplette "Ebene Geometrie". Der durchdachte Aufbau ermöglicht als Ziel der didaktischen Anwendung die plausible Erklärung und Vermittlung der geometrischen Grundlagen.

Ausstattung: 36 geometrische Flächenteile, aufbewahrt in einer übersichtlichen, ferromagnetischen Großmappe (zugeklappt: 37 x 52 cm), ausführliche Lehrerhandreichung. Alle geometrischen Flächen sind magnetisch beschichtet und selbsthaftend.

Stahlmappe mit Aufbewahrungsraster

Demonstrations-Satz Pythagoras G2D/Py 16-teilig in Magnetmappe, aufgeklappt 50x50 cm²

	Der Satz des Pythagoras G2D/OS (Plausibilitätsherleitung)
Mit den 4 roten rechtwinkligen Dreiecken und dem kleinen Quadrat werden das Hypotenusenquadrat und anschließend die beiden Kathetenquadrate abgedeckt.

Magnet-Demonstrations-Satz Kreis K2D
	45-teilig, in Magnetmappe, aufgeklappt 88 x 50 cm² ^{Die großen Kreise haben einen Radius von 10 cm, die kleinen Kreise 5 cm.}

Geometrische Figuren, aufgebaut mit Kreisteilen aus K2D
	^{Die großen Kreise haben einen Radius von 10 cm, die kleinen Kreise 5 cm.}

Magnet-Schülermappe "Pythagoras" Ss/Py 8-teilig, mit 3 strukturierten Arbeitsflächen und einer Aufbewahrungsfläche, Mappe aufgeklappt 40 x 25 cm²
	Magnet-Schülermappe "Geometrie" für die Sekundarstufe GII/OS 23-teilig, mit strukturierter Aufbewahrungsfläche und integrierter Arbeitsfläche. Die Ausstattung beinhaltet 1 Magnet-Spiegellineal. Mappe aufgeklappt 66x33 cm²

Magnet-Demonstrations-Satz "Quadratur des Kreises" Q/K

in Magnet-Aufbewahrungsmappe aufgeklappt 60 x 40 cm², r = 15 cm

Parkettierungen

Magnet Demonstrationsmappe DP/100 100-teilig, aufgeklappt 50 x 50 cm², einheitliche Seitenlänge der Element 5 cm	Magnet-Schülermappe SP/96/B 96-teilig, aufgeklappt 44 x 31 cm², einheitliche Seitenlänge der Element 2,5 cm

Diese Figur ist eine Kombination aus Demo- und Schülersatz.	Diese Figuren sind ausschließlich mit dem Schülersatz aufgebaut.
Obwohl alle Figuren ebene Flächen sind, vermeint unser Auge Körper zu sehen. Es sind jedoch nicht unsere Augen, sondern das Gehirn, das uns diese Wahrnehmung vorgaukelt.

Raumecke
ein entscheidender Fortschritt für den GZ - Unterricht

Die Normalrisse können vom Schüler direkt in die Raumecke gezeichnet und die Fehler leicht korrigiert werden (wasserlösliche Folienschreiber). Das Drehen bzw. Klappen der Bildebenen veranschaulicht dem Schüler den Übergang von der Dreidimensionalität zur Ebene. Ein Zentimeterraster erleichtert die Einordnung von geometrischen Gebilden (Freihandskizzen).

Demonstration starten durch Anklicken!

	Beschriftbar / abwaschbar
	Freihandzeichnungen möglich

Abbildungen entstehen durch Selbsttätigkeit der Schüler. Die Abbildungsreihenfolge der Risse spielt keine wesentliche Rolle.

Zur GEOSET 3D - Raumecke: Risskonstruktionen auf der 3D-Raumecke sind zeitsparend, die Anfertigung von Zeichnungen kann in vielen Fällen entfallen. Punkte bzw. Geraden, die nicht auf einer Ebene liegen, können durch Symbole (Kugel mit Stäbchen) dargestellt werden. Bisher im Unterricht verwendete Modelle sind selbstverständlich verwendbar. Auch im Mathematikunterricht ist die Raumecke einsetzbar. Die Zentimeterrasterung gewährleistet eine anschauliche Einführung in das ebene Koordinatensystem.

Magnet-Raumecke nach Grünwald MRE

Die 3 senkrecht aufeinander stehenden Ebenen sind mit 2 Scharnieren untereinander verbunden und durch einen abnehmbaren Magnetwinkel zu einer Raumecke fixiert. Mit unseren Magnetkörpern kann man jede Fläche der Raumecke besetzen. Darüber hinaus können die Körper unter Verwendung von dafür konstruierten Winkeln beliebig im Raum positioniert werden. Aus den entsprechenden Projektionen ergeben sich dann Grundriß, Aufriß und Seitenriß.

Modellbausatz für die Hand des Schülers
Von der Grundschule bis zum Gymnasium

* GEOSET 63 ermöglicht durch vielfältige Einsatzmöglichkeiten ein breites Arbeitsangebot
für die Hand des Schülers.
* Fördert Kreativität, Raumvorstellungsvermögen und Veranschaulichung.
* Beschriftbar mit wasserlöslichen Folienstiften.

Modellbausatz für die Hand des Schülers - 63 Bauteile: 27 Stk. Würfel, 24 Stk. 1/2 Würfel, 12 Stk. 1/3 Würfel
Bauformen Würfel, Quader, Prismen, beliebig zusammengesetzte Körper, Pyramiden
Einzel-, Partner-, Gruppenarbeit ("Großmodelle")
Individuelle Gestaltung von Modellformen ergibt eine innere Differenzierung und fördert die Selbsttätigkeit in höchstem Maße.
Größte Vielfalt an Variationsmöglichkeiten
Einsatzmöglichkeiten sowohl im Mathematik- als auch im GZ-Unterricht

Die ideale Ergänzung zur Raumecke!

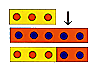
	Minirechner "Geoset 20"
	Ein neues, kompaktes Rechengerät für jeden Schüler der 1.Schulstufe Anwendungsbeispiele:
	1.Ordnen von Zahlen
	2.Nachbarzahlen
		z.B.: Wie heißt der rechte (größere) Nachbar von 9? Wie heißt der linke (kleinere) Nachbar von 9?
	3.Zahlenzwischenraum
		z.B.: Welche Zahlen liegen zwischen 3 und 9? Wieviele Zahlen sind es?
	4.Zahlenzerlegung
	5.Addition
	6.Subtraktion
	7."Wieviel" Rechnungen z.B.: 2 + ? = 9
	8.Visuelles, mengenmäßiges Erkennen

Minirechner ermöglicht:

	Rechenoperationen auf dem Zahlenstrahl 1 - 20
	Rechnungen sind zahlen- und mengenmäßig erfassbar
	Mengenkontrolle auf der Rückseite
	Zehnerüberschreitung optisch erkennbar

	Experimentierbrüche "Geoset 80" Durch das Arbeiten mit Bruchfamilien wird dem Schüler der Einstieg in die Bruchzahlen und das Rechnen mit Brüchen durch "Anschauen und Anfassen" leicht gemacht. Die einzelnen Bruchteile lassen sich zu einer ganzen Scheibe stapeln bzw. stecken und stellen eine kompakte Einheit dar. Anwendungsmöglichkeiten: 1.Zerlegen der Scheiben Erkennung der Teilung Benennen der Bruchteile 2.Übereinanderlegen bzw. Nebeneinanderlegen von Bruchteilen Ordnen der Bruchteile Überprüfen durch Übereinanderlegen Halbiere und verdopple die Brüche 3.Addition von Brüchen in einer Bruchfamilie 4.Subtraktion von Brüchen in einer Bruchfamilie 5.Wie entstehen gleichwertige Brüche (erweitern - kürzen)

	Sektorenbrüche "Geoset 80D" Das ergänzende Demonstrationsmaterial zu Geoset 80. Magnetisch für die Wandtafel. Ferromagnetische Bruchfamilie aufbaugleich wie "Brüche zum Anfassen". Kreisdurchmesser 30 cm.

	Bruchfamilien "Geoset 15" Demobrüche * Veranschaulichung von Bruchfamilien * Mit Brüchen hantieren, Brüche begreifen * Brüche vergleichen - Brüche ordnen * Gemeinsamer Nenner * Rechnen mit Brüchen
		GEOSET 15 Brüche sind in einer ferromagnetischen Aufbewahrungsmappe übersichtlich angeordnet und beinhalten 10 Bruchfamilien.

Bruchzahlenstrahl BZS 110 x 20 cm²

Der BZS ist lieferbar für normale Tafeln mit Aufhängung oder für Stahltafeln magnetisch. Die zur Ausstattung gehörenden Bruchrechenstäbe werden in einem gefächerten, mit Scharnieren versehenen metallischen Aufbewahrungskasten geliefert.

Enthalten sind die Stäbe 1/2, 1/3, 1/4, 1/5, 1/6, 1/8, 1/10, 1/12, 1/15

Das Produkt aus den verschiedenen Nennern und zwei ergibt die Anzahl der zur Ausstattung gehörenden Rechenstäbe (130 St.). Notationskarten zum Einrichten eines speziellen Bruchzahlenstrahles sind auf Wunsch lieferbar. Art.-Nr.: NK

Magnet-Demonstrations-Sätze Maße in cm l / b / h
Bruchteile Rechtecke BT/R in Magnetmappe, aufgeklappt 50 x 50 cm²		Bruchteile Sektoren BT/S in Magnetmappe, aufgeklappt 50 x 50 cm²
BT/R-Ausstattung 1 Ganzes, r = 10 cm dazu passend 2 Halbe, 4 Viertel, 3 Drittel, 6 Sechstel, 5 Fünftel, 10 Zehntel	BT/S-Ausstattung 1 Ganzes, 20 x 20 cm² dazu passend 2 Halbe, 4 Viertel, 3 Drittel, 6 Sechstel, 5 Fünftel, 10 Zehntel

Magnet-Schülermappe Bruchzahlenstrahl SBZS/B aufgeklappt 41 x 19 cm², Ausstattung wie bei BD/BS
Dieser Magnet-Satz soll den Schülern u.a. in die Lage versetzen, experimentell zu erfassen, warum z.B. das Produkt zweier Brüche stets kleiner ist als seine Faktoren. In der Anfangsphase sollen die gerasterten Felder helfen, das Verhältnis der Brüche untereinander und zu ihrem Ganzen zu erkennen.		Die obere Innenseite der Mappe ist mit dem Aufbewahrungsraster für die Rechenstäbe bedruckt. Die untere Innenseite zeigt einen aufgedruckten Bruchzahlenstrahl mit der entsprechenden Arbeitsfläche
	Magnet-Schülermappe Bruchteile SBT/R aufgeklappt 50 x 25 cm2, Ausstattung wie bei BT/R

	Schüler - Rechenrahmen "Geoset 10" Zahlenraum 100, Vollholzausführung

Das Geodreieck
für die Grundschule
"Geoset 14"

	Übersichtliche, lehrplankonforme Gestaltung
	Rechter Winkel durch verschiedene Farben und Symbol deutlich gekennzeichnet
	leichtes Zeichnen von Geraden bzw. Parallelen
	Längenmessung mit durchgehender Skala von 0 bis 14 cm
	Praktisch unzerbrechlich

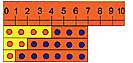
Der Zahlenstrahl ist in einer ferromagnetischen Aufbewahrungsmappe übersichtlich angeordnet.	Grundschul - Zahlenstrahl Zahlenraum 0 bis 30 Unser Grundschul - Zahlenstrahl ermöglicht durch Aufbau und Farbgestaltung eine optimale Hilfe zur visuellen und motorischen Erfassung des Zahlenraumes vom 1. bis zum 3. Zehner!
		Das Auflegen der Mengenstreifen ermöglicht eine anschauliche Durchführung zu - Mengenerfassung - Mengenaufbau - Mengenvergleiche
		Optische Darstellung von - Mengenzerlegung und - Rechenoperationen
		Das Zuordnen von Zahlenstreifen erweckt das grundlegende Verständnis für Zahlen.

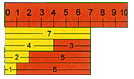
Universal-Zahlenstrahl 0 bis 100

(bzw. bis 1.000.000)

Der jeweilige Zahlenraum, der erarbeitet und durchgliedert werden soll, kann durch die unbeschrifteten Zahlenstreifen selbst gewählt, erstellt und somit auch variiert werden, wodurch der Zahlenstrahl uneingeschränkt in jeder Schulstufe zum Einsatz kommen kann.

Der Zahlenraumbegriff ist Grundvoraussetzung für den Umgang mit Zahlen und zum sinnvollen Durchführen von Rechenoperationen. Ihm kann nicht genug Aufmerksamkeit gewidmet werden!

Es kann wie gewohnt am Zahlenstrahl gearbeitet werden, doch bietet vor allem die Möglichkeit des Übereinanderschichtens der Zahlenplättchen eine neue und effektive Form der Zahlenveranschaulichung.

	Veranschaulichung von Zahlen
	Orientierung im Zahlenraum
	Zahlenreihen / Relationen
	Verständnissentwicklung und -ausbau für den dekadischen Aufbau
	Hinführen zum Lesen und Schreiben von Zahlen

Unterscheiden von Ziffern und deren Stellenwert

Operatives Durchforschen von Zahlen: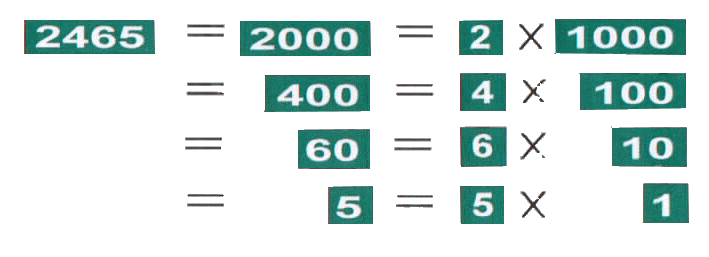

Additives und multiplikatives Zerlegen am Zahlenstrahl oder (vor allem grössere gemischte Zahlen) auch als Plättchenpakete.

Lehrplan: In der Grundstufe II (3. und 4. Stufe) ist der Zahlenraum 1000 bzw. 10000, 100000 und 1000000 vorerst über Grobstrukturen zu erarbeiten! Vor allem in dieser Phase füllt der Universal-Zahlenstrahl eine Lücke, und kommt der Arbeit mit den Plättchenpaketen Bedeutung zu!

Der Zahlenstrahl ist in einer ferromagnetischen Aufbewahrungsmappe übersichtlich angeordnet

alle auf dieser Seite angegebenen Preise sind Verkaufspreise inklusiv der gesetzlich vorgeschriebenen Mehrwertsteuer

Bestellformular